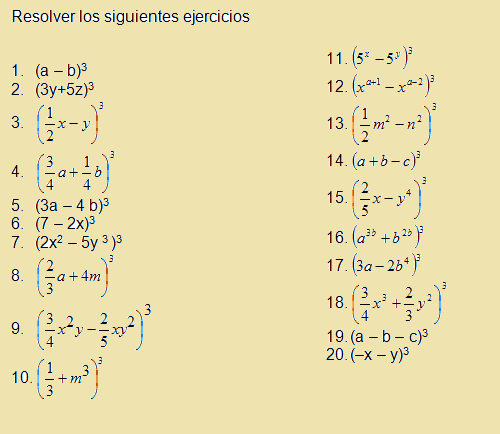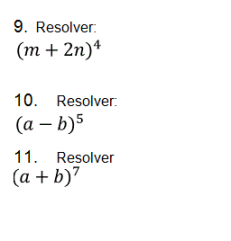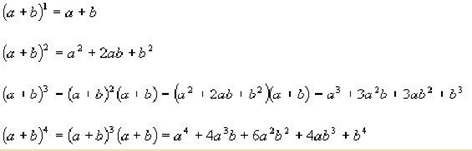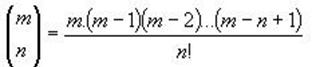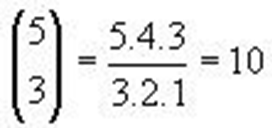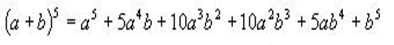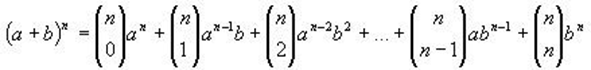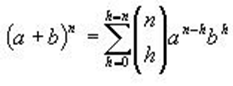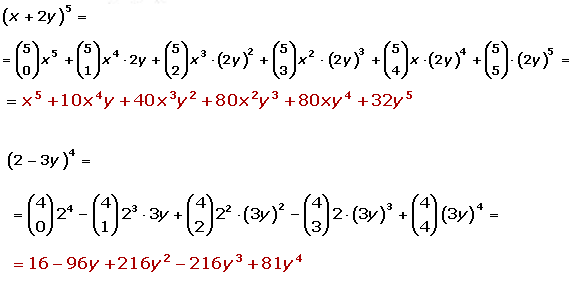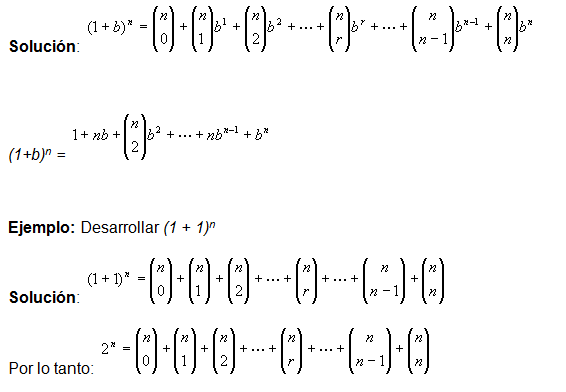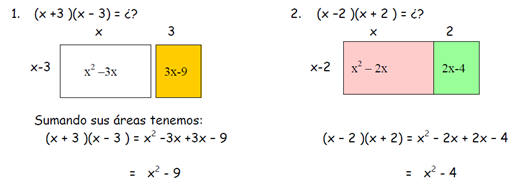BINOMIO DE NEWTON
HISTORIA
El teorema del binomio fue descubierto en el año 1665, fue notificado por primera vez en dos cartas que fueron enviadas por el funcionario y administrativa de la Royal Society, Henry Oldenburg en el año 1676. La primera carta que se tenía fue fechada el 13 de junio de 1676, en respuesta a un pedido del filósofo, jurista y matemático alemán Gottfried Wilhelm von Leibniz, quien quería tener conocimiento de las labores e investigaciones de matemáticos británicos sobre series infinitas. Por lo cual Newton envía el enunciado de su teorema y un ejemplo ilustrativo. Leibniz responde, en una carta fechada el 17 de agosto de 1676, que se encuentra ante una técnica general que le permite obtener distintos resultados sobre las cuadraturas, las series, etc., y denomina algunas de sus ramificaciones por las investigaciones de Leibniz. Newton responde también con una carta en la que detalla cómo ha descubierto la serie de binomios.
(a+b)n
A partir de este hallazgo Newton intuyó que era posible operar con series infinitas del mismo modo que con expresiones polinómicas finitas.
Newton no se encargó de publicar jamás el teorema del binomio. Lo hizo el matemático británico, John Wallis en el año 1685 en su Algebra, en la cual atribuyó a Newton el gran hallazgo.
Un binomio corresponde a un polinomio que se encuentra formado por dos términos. Newton desarrolló la fórmula para así proceder al cálculo de las potencias de un binomio usando para esto números combinatorios. Por medio de esta fórmula se puede formular la potencia que se requiere como la suma de varios términos, cuyos coeficientes se pueden hallar utilizando el triángulo de Tartaglia. Vamos entonces a teorizar la fórmula que nos dejará elevar a una potencia cualquiera de exponente natural, n, un binomio.
Para esto, vamos a ver cómo se desarrollan o las potencias de (a+b).
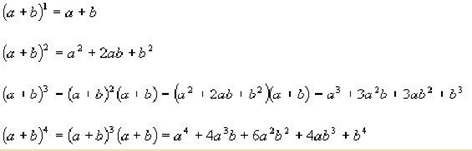
Observando los coeficientes de cada polinomio consiguiente se puede observar el seguimiento de esta secuencia,

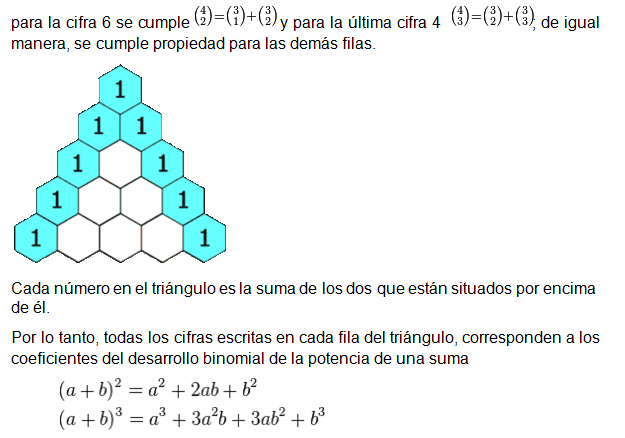
Sería el llamado triángulo de Tartaglia que es obtenido a partir de la notación en filas de los números combinatorios partiendo desde los de numerador 1. Entonces cada una de estas cifras es correspondiente al valor de un número combinatorio, de la siguiente forma:
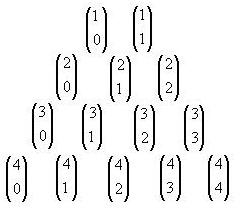
Vemos que cada fila comienza y finaliza en 1 y que los números que figuran forman una fila de modo simétrico, es decir el primero es igual al último, el segundo igual al penúltimo, y así sucesivamente. Cada uno de los números es la suma de los dos que tiene encima.
En cualquier momento se puede encontrar el valor de un número combinatorio cualquiera sea, si recordamos el cálculo con la siguiente fórmula:
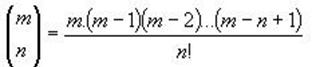
Por ejemplo si se quiere calcular:
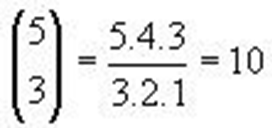
Si prestamos atención a las potencias de (a+b) de nuevo, se puede ver que las potencias de a empiezan elevadas a n, y disminuye uno a uno hasta llegar a cero. Con los exponentes de b acontece lo contrario a esto. Con todo lo anterior ya podemos proceder al cálculo directamente de la siguiente potencia de (a+b), sus coeficientes corresponderán a la fila quinta del triángulo de Tartaglia.
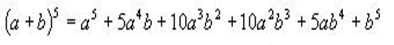
Ahora ya podemos anotar la fórmula general del binomio de Newton, que sería la siguiente:
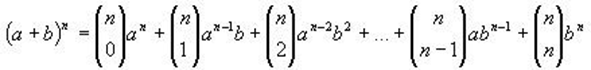
Se puede anotar abreviadamente del siguiente modo,
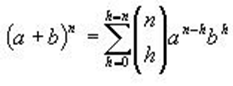
EJEMPLOS
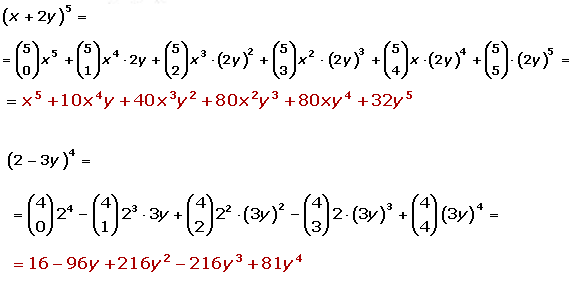





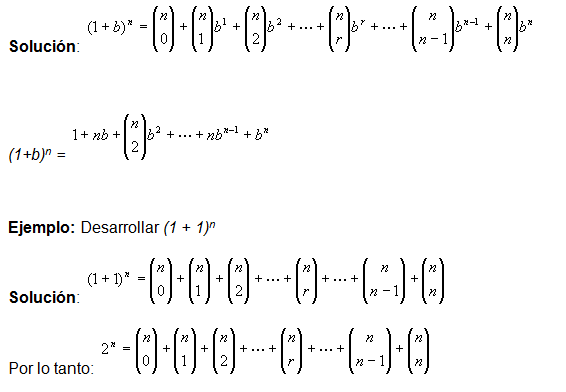


TRIÁNGULO DE PASCAL